Classification: knn

• 「分類」K-Nearest Neighbors (KNN)
• 「K值」的選擇
• [R Code]KNN 範例
• KNN 的優缺點

今天要來講得一樣是解決「分類問題」(Classification)的機器學習方法: KNN。

KNN,全名 (K Nearest Neighbor) K-近鄰演算法，是一種機器學習裡最直觀的方法。簡單上來說，今天如果有一個新資料點出現，模型會去計算距離，並找出最接近的 K 個資料，這 K 個資料中最多的是什麼種類(投票法)就會將新資料點分成那一類。

KNN 是屬於監督式學習(Supervised)的一種，我們train KNN model時，training data需要被標籤(labeled)，也就是資料中要有已知的Y(分類類別)，通常使用的時機是想將新資料進行分類判斷。

[補充] K-Means 是另一種原理很相近的非監督式學習(Un-Supervised)方法，它是聚類的演算法，通常是將還未被標籤(un-labeled)的資料進行「分群」(Cluster)，把資料分成不同的群體、組別。(有時間的話之後會再進行補充。)

「K值」的選擇

在建立 KNN 模型時第一個遇到的問題就是「K」要選則多少?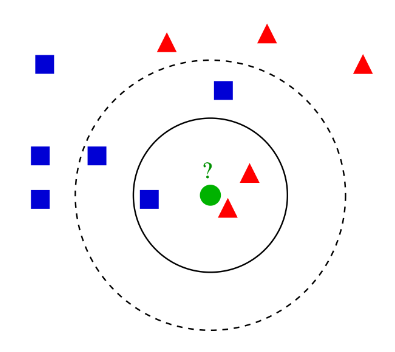

通常「K」會選一個奇數值。因為如果 K 是一個偶數，很容易出現兩個分類類別獲得的票數相同，造成無法判斷的問題。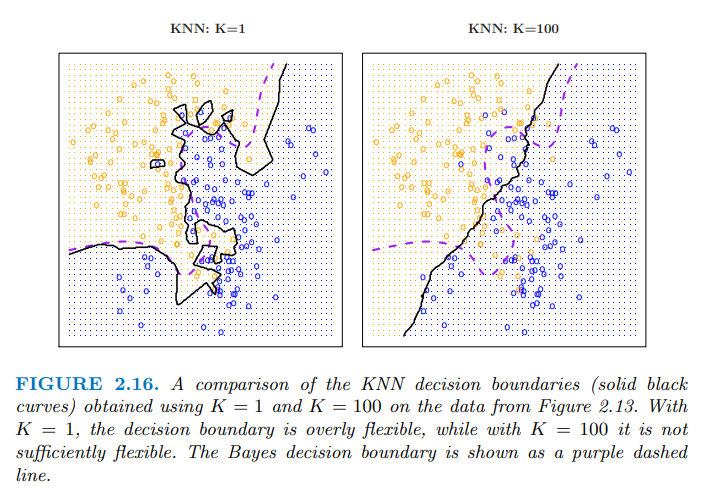

(左圖, k=1)當「K」太小: 會出現overfitting 的問題。
(右圖, k=100)當「K」太大: 會出現underfitting 的問題。
誇張點來說，如果k=n(資料總數)，這個模型相當於沒什麼判斷力了。

總結來說，選擇小的 K ，會比較有彈性(flexible)，有較低的 bias ，但是會有較高的 variance 。
當選擇的 K 增大時，會開始提高 bias 降低 variance ，分類的決策邊界會越來越接近線性分類。

距離的計算方式

• 連續變數:

  • Euclidean Distance (最常被使用)
  • Manhattan Distance
  • Mahalanobis Distance

• 類別變數

  • Hamman
  • Hamming
  • Sokal and Sneath I, III
  • accard similarity

[R Code]KNN 範例

這邊以 Iris dataset 做範例:

#資料切割，隨機把70%當training，30%當testing
data=iris
head(data)   # 觀看前6筆資料
summary(data)# 連續型資料:會看到 Qu.    #類別型資料:會看到不同類別的資料個數 

set.seed(1) # 固定sample()抽樣的結果
train_rows<- sample(x=1:nrow(data), size=ceiling(0.70*nrow(data) ))# 70%的data
train.data<- data[train_rows,] # 70%當training data
test.data <- data[-train_rows,]# 30%當testing data

#從head(data)觀察，前四欄位為我們要用的X，第五欄位"Species"是我們想要的分類的結果Y
train.x<-train.data[,1:4]
test.x<- test.data[,1:4]
train.y<-train.data[,5]
test.y<- test.data[,5]

在 R 裡建立 KNN 模型時，會使用到class 套件和knn( )函式:

installed.packages("class")
library(class)

iris.knn <- knn(train.x, 
                test.x, 
                train.y, # training data 的label
                k = 3)   # k建議設為奇數

iris.knn #test data裡的資料(45筆)，使用knn進行分類的結果

> iris.knn #test data裡的資料(45筆)，使用knn進行分類的結果
 [1] setosa     setosa     setosa     setosa     setosa    
 [6] setosa     setosa     setosa     setosa     setosa    
[11] setosa     setosa     setosa     setosa     setosa    
[16] versicolor versicolor versicolor versicolor versicolor
[21] versicolor versicolor versicolor versicolor versicolor
[26] versicolor versicolor versicolor versicolor versicolor
[31] versicolor versicolor virginica  versicolor virginica 
[36] virginica  virginica  virginica  virginica  virginica 
[41] virginica  virginica  virginica  virginica  virginica 
Levels: setosa versicolor virginica

預測結果與交叉矩陣 Cross table :

# 使用iris.knn對test.x進行"分類的結果"(pred)對照"真實的答案"(test.y)
table(pred=iris.knn, test.y)
mean(iris.knn==test.y)# 分類正確率
(15+17+12)/45         # 分類正確率=斜對角/總資料數

> table(pred=iris.knn, test.y)
            test.y
pred         setosa versicolor virginica
  setosa         15          0         0
  versicolor      0         17         1
  virginica       0          0        12
> mean(iris.knn==test.y)# 分類正確率
[1] 0.9777778
> (15+17+12)/45         # 分類正確率=斜對角/總資料數
[1] 0.9777778

KNN的優缺點

• KNN的優點

1. KNN是一種無母數的分類方法，我們不需要去了解資料的分佈情形，也就是說，再建立分類模型時我們不用去考量分配假設。
2. 資料型態不限（離散、類別型：取眾數。 連續型：取平均值。）
3. 方法直觀好懂。

• KNN的限制

1. KNN在計算上會花費較多時間(需計算所有資料點分群時的距離)以及運算所占記憶體較大(用來預測新資料時，training data所見的模型會佔記憶體)，因此不太適用於資料量較大的數據集。
2. 資料不平衡 (Inbalanced data) 時容易有預測不準確的情形發生。

參考資料、網站、書籍

統計與機器學習 Statistical and Machine Learning, 台大課程. 王彥雯 老師.

ＡＩ專欄, 機器學習演算法 – K 近鄰, 國立政治大學人工智慧與數位教育中心
https://aiec.nccu.edu.tw/ai-column/26

An Introduction to Statistical Learning with Applications in R. 2nd edition. Springer. James, G., Witten, D., Hastie, T., and Tibshirani, R. (2021).